- 1
- 국내산라이츄
- 조회 수 5251
 아... 출근하기 싫다...
아... 출근하기 싫다...
1. 팩토리얼
감마함수에 설명하려면 먼저 팩토리얼에 대해 설명해야 합니다. 보통 n!으로 쓰는데, 이게 뭐냐면
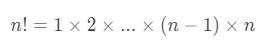
이겁니다. 걍 이거예요. n부터 시작해서 1씩 빼가면서 쫙 곱하는겁니다. 이따가 설명할 이중계승까지 이해하려면 번대 순서(n * (n-1) * ... * 1)로 외우시는 게 좋긴 한데, 뭐 그냥 초항이 1 공차가 1인 등차수열의 n번째 일반항까지 걍 다 곱한다고 보면 됩니다. 백준 재귀함수 파트에도 나오는거예요 이거. (다른 하나는 피보나치 수열과 시어핀스키 카펫)
2. 이중계승
사실 확장 버전으로 다중계승이라는 것도 있는데, 이중계승의 개념을 이해하면 이것도 쉽습니다.
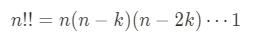
일반적으로 n!이 n에서 시작해서 1씩 빼서 곱하는거고 이중계승은 n에서 2씩 빼서 곱하는겁니다. 즉, 6!은 6부터 1까지 싹 곱하는거고 6!!은 6, 4, 2를 곱하는겁니다. (다중계승은 느낌표 여러개 붙여서 표기합니다) 대신 이중계승은 n이 홀수냐 짝수냐에 따라 종점이 달라집니다.
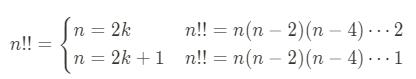
n이 짝수일 때는 2, 홀수일때는 1에서 끝납니다. 이것도 그것만 처리 잘 해주면 코딩하는 건 어렵지 않습니다.
근데 우리 감마함수 한다매 왜 팩토리얼이 나와요? 아 좋은 질문입니다. 고돡교 수학과정에서 팩토리얼 하면 순열조합 세트가 나올겁니다. 자, 여기서 잘 생각해보세요. 순열조합 할 때 nPr 혹은 nCr의 n이나 r에 소수(정수가 아닌 유리수)가 들어가는 거 보셨나요? 그럼 음수는요? 아 당연히 못봤죠. 왜냐하면 정수가 아닌 유리수와 음수는 팩토리얼이 존재하지 않으니까요.
정확히 말하자면, 정수가 아닌 유리수는 팩토리얼이 없는 게 아니라 우리가 일반적으로 고돡교 수학 과정에서 배웠던 방식으로 구할 수 없는겁니다. 음수는 그냥 팩토리얼이 없어요.
3. 감마함수
감마함수는 팩토리얼의 상위호환격 함수입니다.
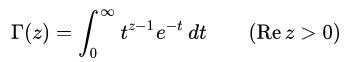
이런 수식을 가지고 있는데... 으아아 내눈 누가 적분좀 치워주세요 저거 심지어 이상적분이야 아이 저거는 나도 했어요 sympy 때려박으면 다돼 다. 그 전에 울프램알파로 가시죠 아 그러네 알파신 있지
아무튼 저런 수식을 가지고 있는데... 적분기호에 왜 무한대가 있냐면 저건 이상적분이기 때문입니다. (뭔지는 모르지만 이상적분이라고 부름) 감마함수가 팩토리얼의 상위호환이라서 저기다가는 정수가 아닌 유리수나 복소수(허수 붙어있는 그거 맞음)를 때려박아도 팩토리얼을 구해줍니다. 대신, 감마함수의 성질을 잘 이용해야 해요.
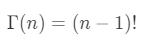
감마함수는 이런 성질을 가지고 있어서, 6!을 구하고 싶으면 7을 넣어야 합니다. 1.5!을 구할거면 1을 더한 2.5를 때려박으면 되고, 1+i!을 구할거면 실수부에 1을 더해서 2+i를 넣으면 됩니다. 어째서인지는 모르겠으나 실수부가 음수인 복소수도 알파신 통해서 저기다 때려박으면 뭐가 나오긴 나옵니다. 복소수라 글치.
어? 그럼 상위호환인데 음수도 되나요? 허수 꼬리가 안 붙는 음수는 감마함수의 정의역에 존재하지 않습니다. 감마함수는 0 이하(0과 음의 정수)를 때려박으면 미쳤습니까 휴먼? 합니다. 알파신에서 때려박으면 무한대가 나오고 Sympy에 때려박으면 에러 뜹니다. (Sympy는 0 때려박으면 에러는 안 나는데 뭔 괴랄한 게 반깁니다) 팩토리얼의 상위 호환이라는 그 감마함수도 0과 음수는 아 이건 좀... 하기 때문에 음수는 감마함수 할아버지가 와도 팩토리얼이 없다고 보시는 게 맞습니다.
생각해보면, nPr(순열)은 n개에서 r개를 순서대로 꺼내는거고 nCr(조합)은 n개에서 r개를 순서 없이 걍 집는건데 거기서 음수가 나오면 그것도 이상하잖아요? 6개에서 -2개를 어떻게 집겠습니까. 2개 넣으면 된다 아 그런가 근데 그렇게 따지면 소수도 마찬가지다
appendix. 이걸 진짜 코딩한거 실화고요
1) 감마함수
from sympy import *
from mpmath import mp
import sys
a = complex(sys.stdin.readline())
# 복소수는 complex로 입력해야 합니다. (int: 정수, float: 소수라고 생각하면 됨)
t = symbols("t")
expr = t ** (a - 1) * exp(-t)
gamma_function = integrate((expr),(t,0,oo))
if a.real > 0 and a.imag == 0:
if gamma_function % 1 == 0:
print(round(gamma_function))
else:
print(round(gamma_function,3))
else:
print("Cannot calculate Gamma function")
아니 이걸 진짜 했네 했다니까요
2) 계승(일반 계승)
from sympy import *
from mpmath import mp
import sys
def gamma_function(a):
t = symbols("t")
expr = t ** (a - 1) * exp(-t)
if a.real > 0:
return integrate((expr),(t,0,oo))
else:
return False
a = float(sys.stdin.readline().strip())
# Factorial(계승): 일반적으로 n! = 1*2*3*...*n-1*n이다. (5!=1*2*3*4*5)
factorial = 1
if a < 0:
print("Can't calculate factorial")
# 음수는 factorlal이 없음
elif a == 0:
print(factorial)
# 0! = 1
elif a % 1 != 0:
print(round(gamma_function(a+1),3))
else:
for i in range(int(a),0,-1):
factorial *= i
print(factorial)
For, 일반 계승
from sympy import *
from mpmath import mp
import sys
def gamma_function(a):
t = symbols("t")
expr = t ** (a - 1) * exp(-t)
if a.real > 0:
return integrate((expr),(t,0,oo))
else:
return False
a = float(sys.stdin.readline().strip())
# 와 팩토리얼이 생각보다 빡센거였구나...
# Factorial(계승): 일반적으로 n! = 1*2*3*...*n-1*n이다. (5!=1*2*3*4*5)
factorial = 1
if a < 0:
print("Can't calculate factorial")
# 음수는 factorial이 없음
elif a == 0:
factorial = 1
# 0! = 1
elif a % 1 != 0:
print(round(gamma_function(a+1),3))
else:
while a >= 1:
factorial *= a
a -= 1
print(factorial)
While, 일반계승
3) 이중계승
import sys
a = float(sys.stdin.readline())
factorial = 1
if a < 0:
print("Can't calculate factorial")
elif a == 0 or a == 1:
print(factorial)
# 0! = 1
elif a % 1 != 0:
print("정수가 아닌 유리수는 일반적인 방법으로 팩토리얼을 구할 수 없습니다. ")
else:
for i in range(int(a),0,-2):
factorial *= i
print(factorial)
For, 이중계승
import sys
a = float(sys.stdin.readline())
factorial = 1
if a < 0:
print("Can't calculate factorial")
elif a == 0 or a == 1:
print(factorial)
# 0! = 1
elif a % 1 != 0:
print("정수가 아닌 유리수는 일반적인 방법으로 팩토리얼을 구할 수 없습니다. ")
else:
while a > 0:
factorial *= a
a -= 2
print(factorial)
While, 이중계승(이중계승은 일반 계승과 달리 자연수만 됩니다)
4) 계승 소수
import sys
a = float(sys.stdin.readline())
# 역사와 전통의 그거 맞음
def factorial(a):
factorial = 1
if a < 0:
return False
elif a == 0:
factorial = 1
return factorial
elif a % 1 != 0:
return False
else:
for i in range(int(a),0,-1):
factorial *= i
return factorial
# Factorial 구하는 로직(...)
def isprime(a):
sqrt = int(a ** 0.5)
if a < 2:
return False
for i in range(2,sqrt+1):
if a % i == 0:
return False
else:
return True
# 소수 정의 함수
plus_factorial = factorial(a) + 1
minus_factorial = factorial(a) - 1
if isprime(minus_factorial) and isprime(plus_factorial):
print("{}! - 1, {}! + 1 둘 다 {}, {}로 계승 소수입니다. ".format(a,a,minus_factorial,plus_factorial))
elif isprime(minus_factorial):
print("{}! - 1이 {}로 계승 소수입니다. ".format(a,minus_factorial))
elif isprime(plus_factorial):
print("{}! + 1이 {}로 계승 소수입니다. ".format(a,plus_factorial))
else:
print("{}! - 1, {}! + 1 둘 다 {}, {}로 계승 소수가 아닙니다. ".format(a,a,minus_factorial,plus_factorial))
계승 소수는 n!-1 혹은 n!+1이 소수인 걸 계승 소수라고 합니다. (n!-1과 n!+1이 둘 다 계승소수인 경우도 있습니다. 대표적으로 3)





정독 해보겠습니다